15.2.2 De ideale gaswet

De toestandsvergelijking van een ideaal gas is

$$ p \cdot V = n \cdot R \cdot T.$$

Hierbij is

• P  de druk van het gas, in pascal (Pa);
• V  het volume van het gas, in m³;
• n  de hoeveelheid gas, in mol;
• R = 8,3145 J/mol K, de gasconstante;
• T  de absolute temperatuur, in kelvin (K).

Een mol is gelijk aan $6,022 \cdot 10^{23}$ deeltjes. (Eventueel kan men ook met het aantal moleculen werken (N); in dat geval is $p \cdot V = N \cdot k \cdot T$, waarbij k de constante van Boltzmann is, $k= 1.38 \cdot 10^{–23} \; \text{J/K}.$)

Uit de ideale gaswet kan men een aantal belangrijke conclusies trekken:

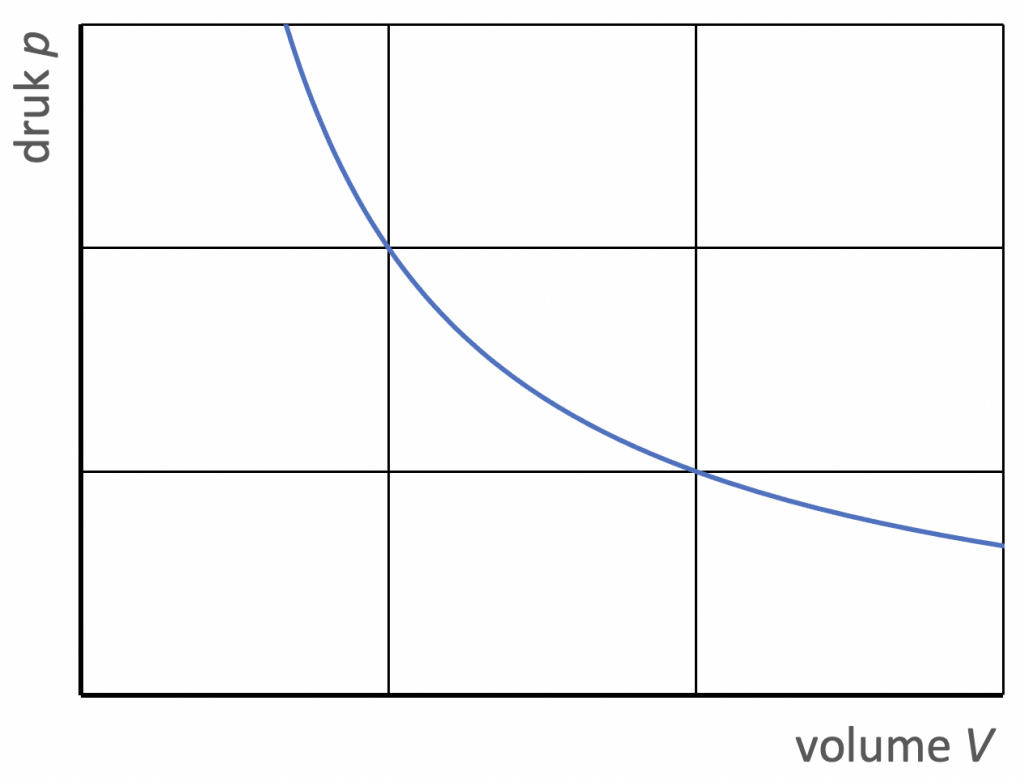
1. Als de temperatuur van een gas constant is, geldt:

$$ p \cdot V = \text{constante} \ \ \ \ \ (T\;\text{constant}).$$

Dit is de wet van Boyle. In dit geval zijn druk en volume dus omgekeerd evenredig: verdubbeling van de druk leidt tot halvering van het volume, enzovoort.

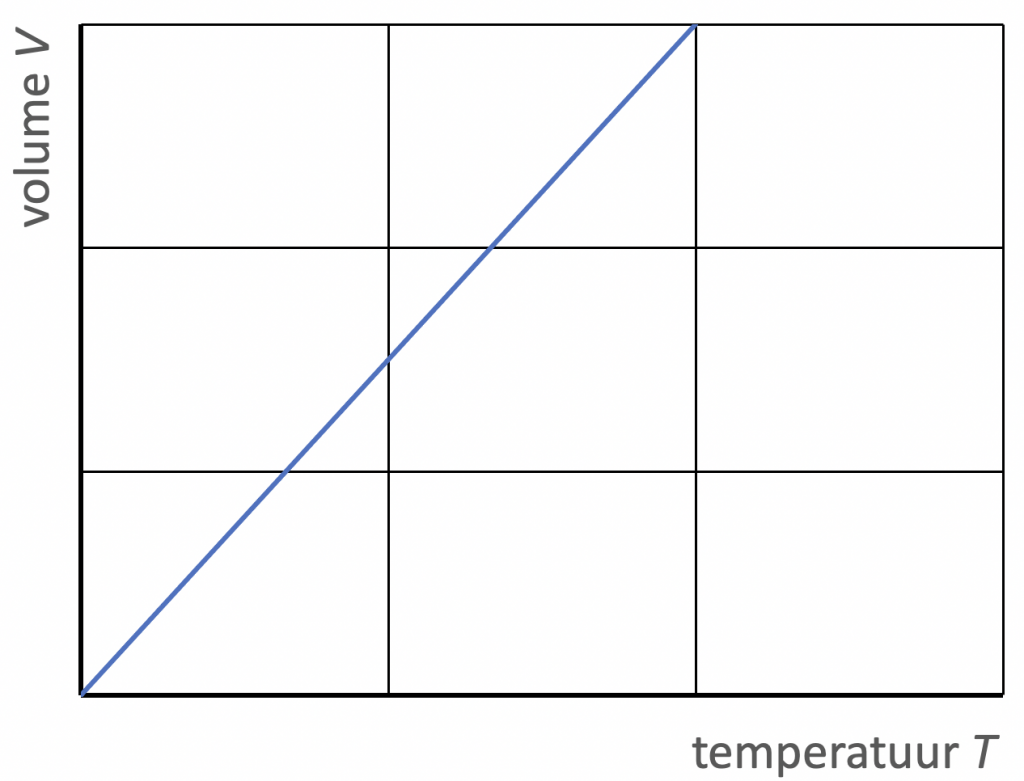
2. Als de druk van een gas constant is, geldt $$\frac{V}{T} = \text{constante} \ \ \ \ \ \ (p \; \text{constant})$$

Dit is de volumewet van Gay-Lussac, of ook de wet van Charles. Het volume van een gas is dus recht evenredig met de absolute temperatuur.

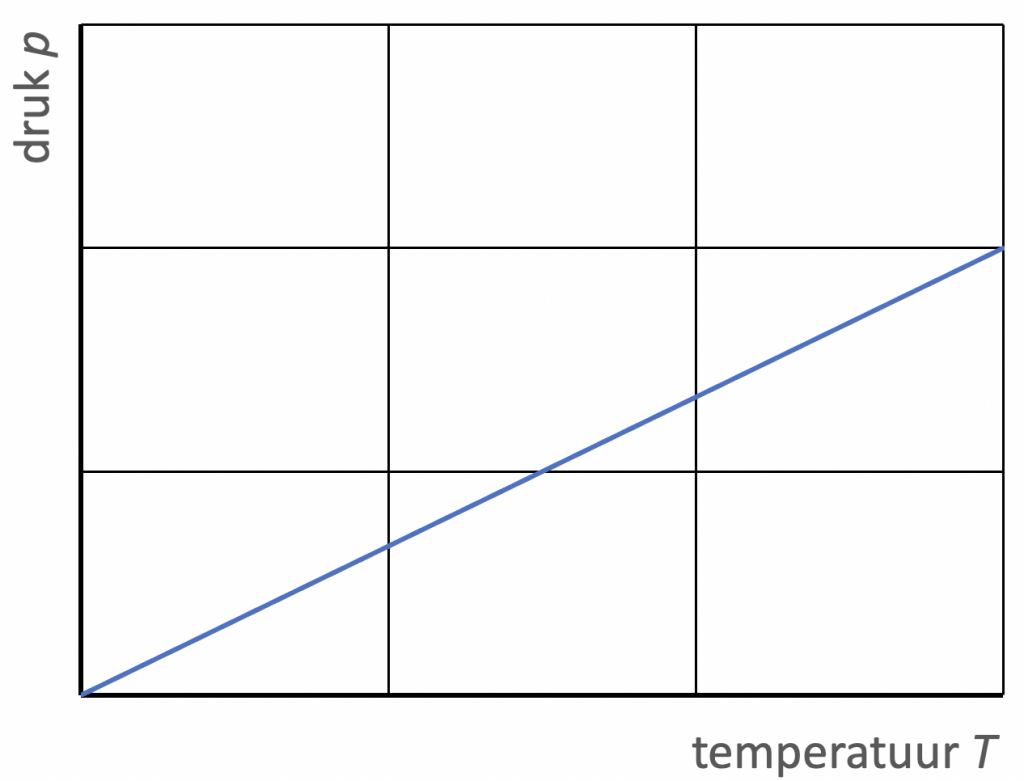
3. Als het volume van een gas constant wordt gehouden (bijvoorbeeld in een stalen vat), dan geldt $$\frac{p}{T} = \text{constant}. \ \ \ \ \ \ (V \; \text{constant})$$

Dit is de (druk)wet van Gay-Lussac. De druk van een gas is dus recht evenredig met de absolute temperatuur.

De ideale gaswet bevat geen grootheden die afhangen van het soort deeltje. Alle gassen hebben dus vergelijkbaar fysisch gedrag. Wel kunnen gassen verschillen in dichtheid (afhankelijk van de massa van de moleculen), in warmtecapaciteit, en in chemische eigenschappen.