De vervangingsweerstand van een schakeling is de weerstand die de schakeling als geheel blijkt te hebben.
In een serieschakeling geldt $$R_{\text{vervanging}} = R_1 + R_2 + R_3 + …$$
In een parallelschakeling geldt $$\frac{1}{R_{\text{vervanging}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + …$$
Voorbeeld: Een weerstand van 8 Ω is in serie geschakeld met een elektromotor van 2 Ω. Deze schakeling wordt vervolgens aangesloten op een 9,0 V batterij. Bepaal de vervangingsweerstand en de stroomsterktes en spanningen voor beide toestellen.
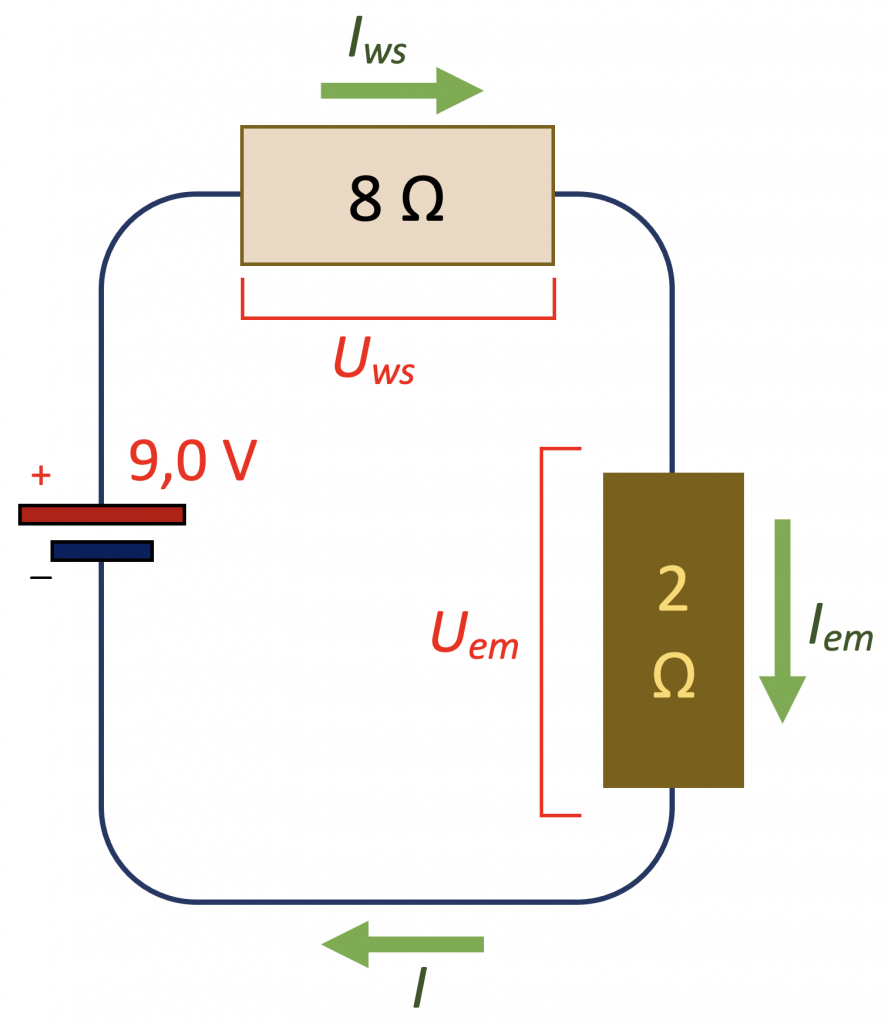
De vervangingsweerstand is
$$R_{\text{vervanging}} = 8 \; \Omega + 2 \; \Omega = 10 \; \Omega.$$
De stroom die door de schakeling gaat lopen is daarom gelijk aan
$$I_{\text{schakeling}} = \frac{U_{\text{schakeling}}}{R_{\text{vervanging}}} = \frac{9{,}0 \; \text{V}}{10 \; \Omega} = 0{,}9 \; \text{A}.$$
In een serieschakeling zijn alle stromen gelijk, dus
$$I_{ws} = 0,9 \; \text{A}; \; \; I_{em} = 0{,}9 \; \text{A}.$$
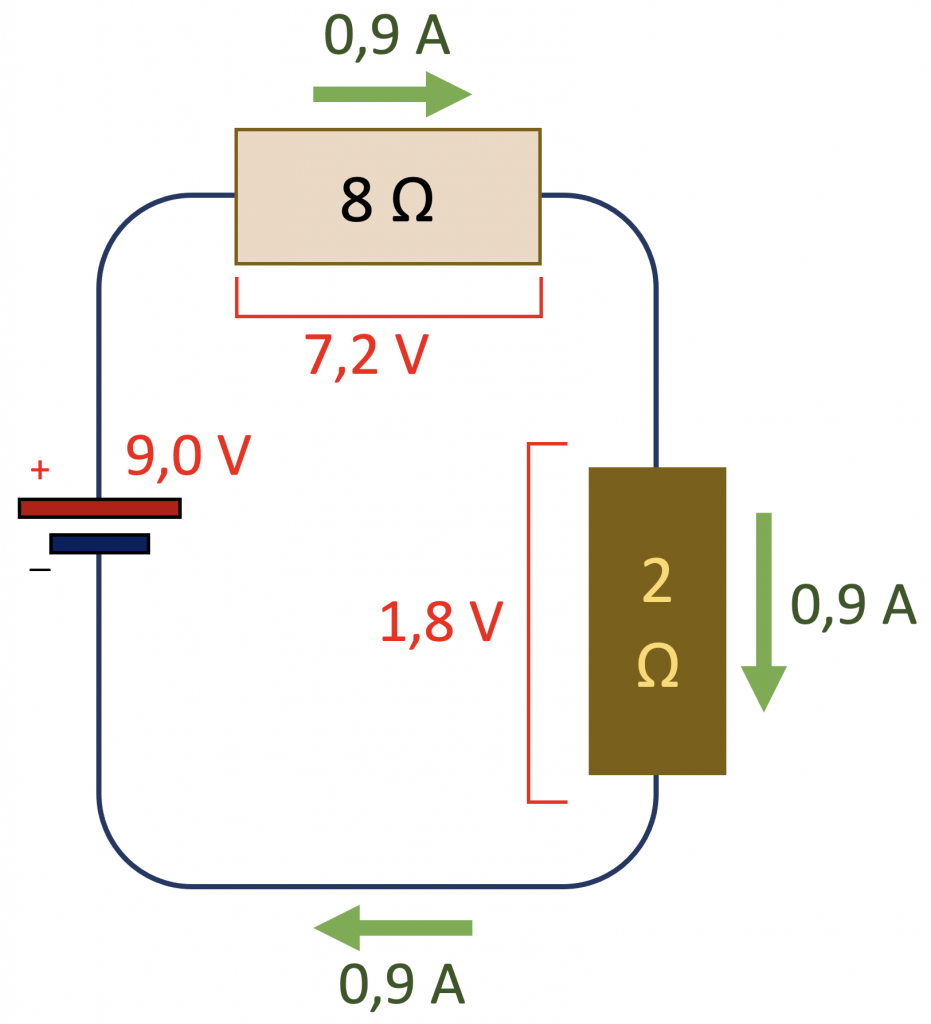
De totale spanning van 9,0 V wordt verdeeld over de toestellen, maar niet gelijkelijk: het toestel met de grootste weerstand heeft de meeste spanning nodig:
$$\begin{align}
U_{ws} = I_{ws}R_{ws} & = 0{,}9 \; \text{A} \cdot 8 \; \Omega = 7{,}2 \; \text{V}; \\
U_{em} = I_{em}R_{em} & = 0{,}9 \; \text{A} \cdot 2 \; \Omega = 1{,}8 \; \text{V}.
\end{align}$$
Voorbeeld: Een warmhoudplaat met een weerstand van 45 Ω en een schemerlamp van 36 Ω zijn aangesloten op hetzelfde stopcontact met U = 180 V in parallelschakeling. Bepaal de vervangingsweerstand en de stroomsterktes en spanningen.
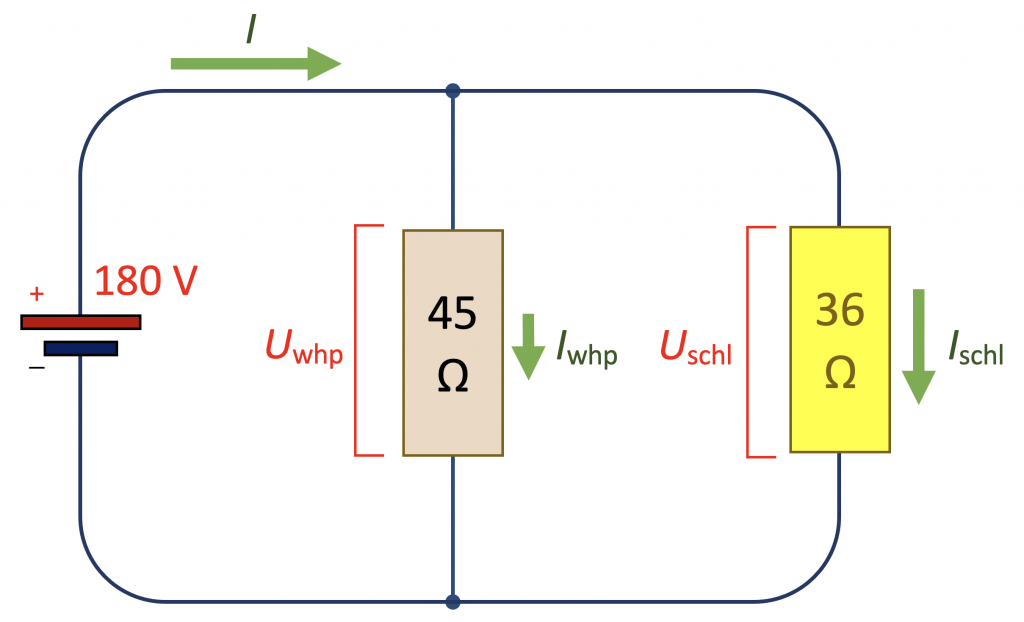
De vergelijking voor de vervangingsweerstand wordt:
$$\frac{1}{R_{\text{vervanging}}} = \frac{1}{45 \; \Omega} + \frac{1}{36 \; \Omega} = \frac{4}{180 \; \Omega} + \frac{5}{180 \; \Omega} = \frac{9}{180 \; \Omega} = \frac{1}{20 \; \Omega};$$
zodoende is Rvervanging = 20 Ω.
De totale stroomsterkte is dus
$$I_{\text{schakeling}}=\frac{U_{\text{schakeling}}}{R_{\text{vervanging}}} = \frac{180 \; \text{V}}{20 \; \Omega} = 9,0 \; \text{A}.$$
Beide toestellen ontvangen de volle 180 V spanning.
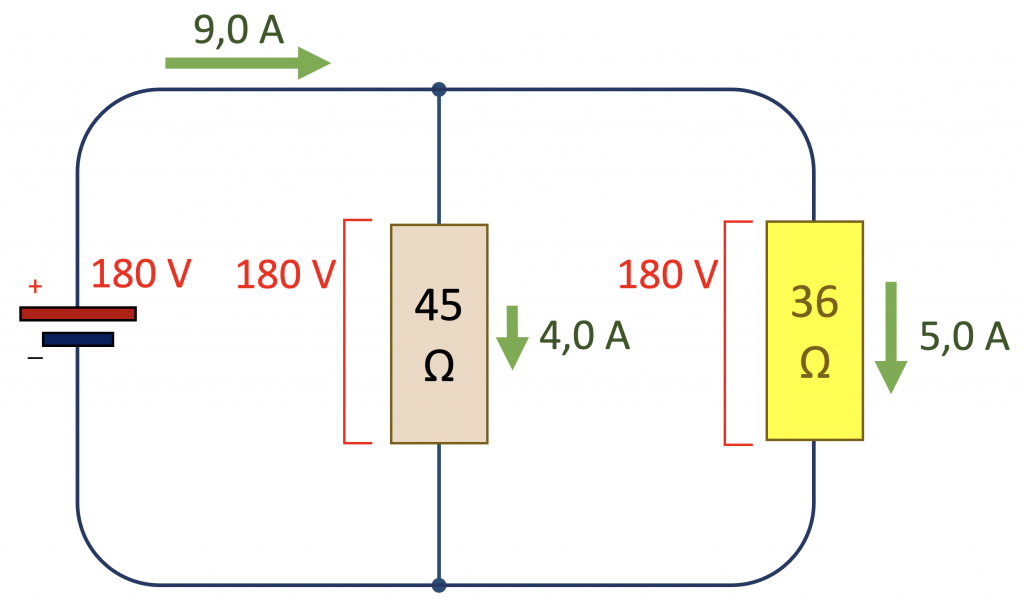
De 9,0 A totale stroom wordt verdeeld over de toestellen; het toestel met de laagste weerstand krijgt de meeste stroom:
$$\begin{align}
I_{whp} = \frac{U_{whp}}{R_{whp}} & = \frac{180 \; \text{V}}{45 \; \Omega} = 4{,}0 \; \text{A}; \\
I_{schl} = \frac{U_{schl}}{R_{schl}} & = \frac{180 \; \text{V}}{36 \; \Omega}= 5{,}0 \; \text{A}.
\end{align}$$
