Volgens de kwantummechanica is het verval van instabiele kernen een onvoorspelbaar toevalsproces. Echter, de kans dat een kern zal vervallen in de volgende seconde, minuut, of dag, is wel een vast getal. Doordat zelfs een kleine hoeveelheid radioactief materiaal zeer veel atomen bevat, heeft het verval op grote schaal een zeer regelmatig gedrag.
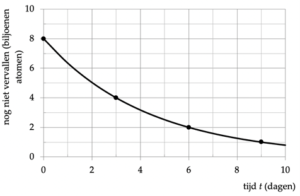
Het aantal nog niet vervallen atomen neemt exponentieel af. Dit gedrag wordt hieronder in een grafiek geïllustreerd. Het vervalgedrag wordt gekarakteriseerd door de zgn. halfwaardetijd (thw). Dit is de tijd waarin naar verwachting de helft van de atomen vervallen zal zijn.
Na twee halfwaardetijden zal een vierde deel van de kernen nog niet vervallen zijn; na drie halfwaardetijden nog maar een achtste deel; enzovoort. Dit kan wiskundig worden uitgedrukt in de vergelijking
$$N_t = N_0 \cdot \left(\frac{1}{2}\right)^{t/t_{hw}}.$$
Hierbij staat N0 voor het oorspronkelijke aantal kernen, en Nt voor het aantal dat nog niet is vervallen na een tijdsduur t.
In de grafiek hierboven is de halfwaardetijd 3 dagen, omdat na drie dagen van de 8 biljoen atomen nog maar 4 biljoen over zijn. Na nogmaals 3 dagen is het aantal weer gehalveerd, tot 2 biljoen; enzovoort.
Halfwaardetijden kunnen zeer kort zijn (nanoseconden) maar ook zeer lang (biljoenen jaren).
Voorbeeld: Stel we hebben 128,0 mg van de betastraler goud-200. Na precies vier uur is er nog maar 4,0 mg van deze stof over. Wat is de halfwaardetijd?
De oorspronkelijke hoeveelheid is gedeeld door 32; dat zijn vijf halveringen (32 = 25). Blijkbaar is $5 \cdot t_{hw} = \text{4 uur = 240 minuten}$. Hieruit volgt dat de halfwaardetijd van goud-200 gelijk is aan thw = 48 minuten.
