Nu beschouwen wij het geval waarin een voorwerp zich langs een rechte lijn beweegt met een constante versnellingsvector a. Dit heet eenparig versnelde rechtlijnige beweging (EVRB). Opnieuw nemen wij aan dat het beginpunt x0 = 0. Het is mogelijk dat het voorwerp een beginsnelheid v0 heeft. Nu geldt er
$$a = \; \text{constant}$$
$$v = a \cdot t + v_0$$
$$x = \frac{1}{2} at^2 + v_0t.$$
Voorbeeld: Een hockeypuck beweegt met een snelheid van 8,8 m/s, maar vertraagt geleidelijk met 1,2 m/s per seconde. Maak een tabel met de snelheid en positie van de puck voor de eerste zes seconden van deze beweging.
Het ligt voor de hand de huidige bewegingsrichting als positief te beschouwen. De puck vertraagt; dit betekent dat de versnelling tegengesteld is aan de snelheid, ofwel negatief. Dus hebben wij EVRB met a = –1,2 m/s2 en v0 = +8,8 m/s:
$$v = -1,2t + 8,8;$$
$$x = -0,6t^2 + 8,8t.$$
| t (s) | v (m/s) | x (m) |
|---|---|---|
| 0,0 | 8,8 | 0,0 |
| 1,0 | 7,6 | 8,2 |
| 2,0 | 6,4 | 15,2 |
| 3,0 | 5,2 | 21,0 |
| 4,0 | 4,0 | 25,6 |
| 5,0 | 2,8 | 29,0 |
| 6,0 | 1,6 | 31,2 |
Deze formules leveren de volgende tabel:
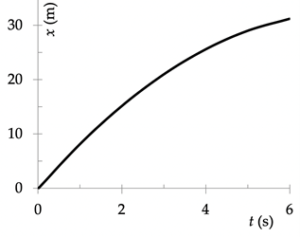
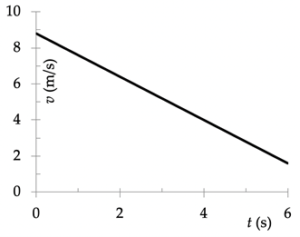
De grafieken x(t) en v(t) die bij deze beweging horen zijn karakteristiek voor EVRB. De positiegrafiek een parabool; de snelheidsgrafiek is een rechte lijn.