Men komt vaak situaties tegen waarbij een versnellend voorwerp begint in rust. Het komt relatief langzaam op gang en beweegt steeds sneller. De bijbehorende grafieken zijn als volgt:
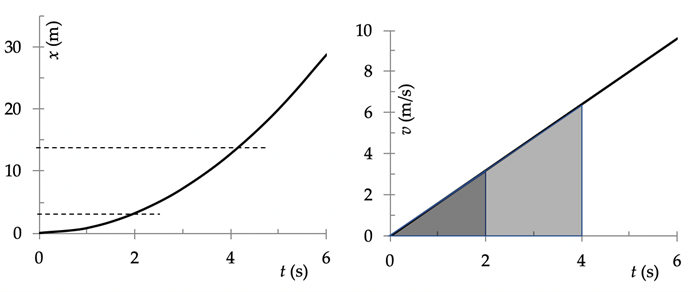
De afgelegde weg is hier evenredig met het kwadraat van de tijd. Als het voorwerp tweemaal zo lang onderweg is, legt het een viermaal zo grote afstand af. De snelheid is echter recht evenredig met de tijd.
Voorbeeld: Een vallend voorwerp is in eenparig versnelde beweging vanuit rust. Het landt op de grond met een snelheid van 20,0 m/s. Hoe snel beweegt het als het de helft van de afstand heeft afgelegd?
Omdat de afstand evenredig is met het kwadraat van de tijd, weten wij dat $\sqrt{\frac{1}{2}} \approx 71$ (71%) van de tijd verstreken is. Omdat de snelheid recht evenredig is met de tijd, heeft het voorwerp ook 0,71 (71%) van zijn eindsnelheid bereikt. De snelheid is dus $0,71 \cdot 20,0 = 14 \; \text{m/s}.$
