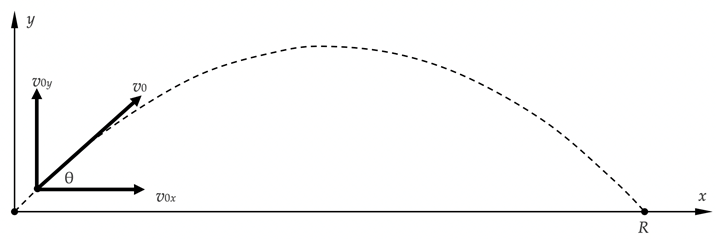
Een diagonaal geworpen projectiel behandelt men net zo als een horizontaal geworpen projectiel; nu is er echter ook een beginsnelheid in de y-richting. Ditmaal kiezen wij de positieve y-richting naar boven; ook kiezen wij weer het beginpunt in de oorsprong.
Opnieuw heeft met ERB in horizontale richting, en EVRB verticaal:
$$v_x = v_{x0} \ \ \ \ \ x = v_{x0} \; t$$
$$v_y = v_{y0} – g \; t \ \ \ \ \ y = v_{y0} \; t – \frac{1}{2} g \; t^2$$
Vaak worden de grootte en richting van de beginsnelheid gegeven. Als θ de hoek is tussen de beginrichting en de x-richting, dan geldt
$$v_{0x} = v_0 \cos{\Theta}; \ \ \ \ \ v_{0y} = v_0 \sin{\Theta}.$$
Voor het bepalen van het hoogste punt gaat men te werk als voor een verticaal projectiel: stel vy = 0 en los op voor t.
Ook van belang is de vraag hoe ver een projectiel in horizontale richting reikt, aangenomen dat het landt op dezelfde hoogte als waar het begon. Men vindt
$$R = v^2_0 \sin{(2\Theta)}.$$
Hieruit volgt ook dat een projectiel het verste gaat als het wordt gelanceerd onder een hoek van 45˚.
Voorbeeld: Een kanonskogel wordt afgeschoten met een snelheid van 40 m/s onder een hoek van 35˚ met de grond. Analyseer de beweging.
Componenten van de beginsnelheid:
$$v_{0x} = 40 \cdot \cos{35^\circ} = 82,8 \; \text{m/s in voorwaarse richting}.$$
$$v_{oy} = 40 \cdot \sin{35^\circ} = 22,9 \; \text{m/s in opwaartse richting}.$$
Vergelijkingen van de beweging:
$$v_x = 32,8 \ \ \ \ \ x = 32,8 \cdot t.$$
$$v_y = 22,9 – 9,8 \cdot t \ \ \ \ \ y = 22,9 \cdot t – 4,9 \; t^2.$$
Hoogste punt:
$$0 = v_y = 22,9 – 9,8 \cdot t \ \ \ \Rightarrow \ \ \ t = 2,34 \; \text{s}.$$
Op dat tijdstip geldt
$$x = 32,8 \cdot 2,34 = 76,7 \; \text{m} \ \ \ \text{(horizontale afstand van beginpunt)}.$$
$$y = 22,9 \cdot 2,34 \; – 4,9 \cdot 2,342 = 26,9 \; \text{m} \ \ \ \text{(hoogte boven beginpunt)}.$$
$$v_x = 32,8 \; \text{m/s} \ \ \ \text{(snelheid op hoogste punt)}.$$
Landing op de grond:
Van hoogste punt naar de grond duurt even lang als van beginpunt naar hoogste punt: in totaal dus
$$t = 2 \cdot 2,34 = 4,68 \; \text{s}.$$
Op dat tijdstip is
$$x = 32,8 \cdot 4,68 = 153 \; \text{m} \ \ \ \text{(afstand van beginpunt)}.$$
$$v_x = 32,8 \; \text{m/s} \ \ \ \text{(snelheid bij landing)}.$$
$$22,9 – 9,8 \cdot 4,68 = \; -22,9 \; \text{m/s}.$$
De snelheidsvector is het spiegelbeeld van de beginsnelheid: de kogel landt met 40 m/s snelheid, en maakt weer een hoek van 35˚ met de grond.
Tenslotte, was de kanonskogel gelanceerd onder de optimale hoek van 45˚, dan zou hij net iets verder gegaan zijn (163 m), maar beduidend langer onderweg zijn geweest: 5,77 s.
