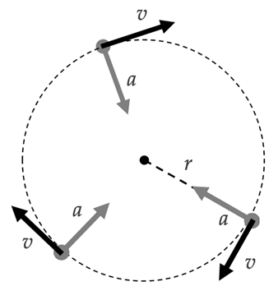
In eenparige cirkelvormige beweging is slechts de grootte van de snelheid constant is. De snelheidsvector staat steeds loodrecht op de voerstraal die het voorwerp verbindt met het middelpunt van de cirkel. Aangezien die voerstraal draait, draait de snelheidsvector ook. Omdat de snelheidsvector voortdurend verandert, is er sprake van versnelling.
Er is hier sprake van centripetale (middelpuntzoekende) versnelling. In ECB staat de versnellingsvector loodrecht op de bewegingsrichting, en wijst naar het middelpunt van de cirkel.
De grootte van de centripetale versnelling is:
$$a_{cp} = \frac{v^2}{r}.$$
Voorbeeld: Een auto rijdt met een snelheid van 25 m/s door een cirkelvormige bocht met een straal van 120 meter. Bepaal de centripetale versnelling.
We hebben ECB, met v = 25 m/s en r = 120 m.
$$a_{cp} = \frac{v^2}{r} = \frac{(25\; \text{m/s})^2}{120 \; \text{m}} = 5,3 \; \mathrm{m/s^2}.$$
Dit is een forse versnelling: meer dan de helft van de valversnelling g. Inzittenden zullen deze versnelling zeker voelen.
