Als een voorwerp op een helling staat, wijst de normaalkracht niet meer recht omhoog. Zij kan daarom de zwaartekracht niet precies tegenwerken. Er blijft een resultante kracht over, die langs te helling omlaag wijst. Als gevolg hiervan, neigt een voorwerp naar beneden te glijden. Of dit wel of niet gebeurt, hangt af van eventuele wrijvingskrachten die de helling op het voorwerp uitoefent.
In de tekening hieronder zijn de drie relevante krachten getekend.
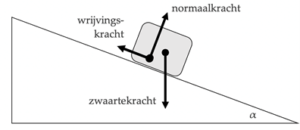
- De zwaartekracht (van de aarde) wijst omlaag en is gelijk aan $m \cdot g$.
- De normaalkracht Fn (van de helling) wijst loodrecht op de helling. Zij is precies sterk genoeg om te voorkomen dat het voorwerp in de helling doordringt.
- De wrijvingskracht Fw (van de helling) wijst evenwijdig de helling op.
De steilheid van een helling wordt beschreven door de hellingshoek α.
Het is nuttig om een coördinatenstelsel te gebruiken waarin x evenwijdig aan de helling is, en y loodrecht daarop staat. We weten dan namelijk dat Fn enkel in de y-richting wijst, en Fw in de x-richting. De zwaartekracht moet nu wel ontbonden worden in twee componenten:
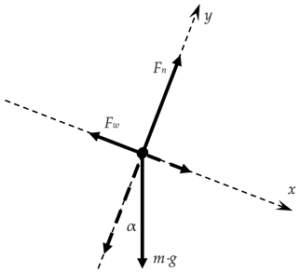
De normaalkracht zorgt ervoor dat het voorwerp zich alleen in de x-richting kan bewegen; dus kan er op zijn hoogst een resultante kracht bestaan in de x-richting.
Wij schrijven nu vergelijkingen uit voor beide componenten van de resultante kracht:
$$\begin{align} x-\text{richting}:\ \ \ & F_{res} = mg \sin{\alpha} \; – F_w; \\ y-\text{richting}:\ \ \ & 0 = F_n \; – mg \cos{\alpha}.\end{align}$$
Wij hebben hier gebruik gemaakt van goniometrie om de componenten van de zwaartekracht uit te werken. Let ook op het gebruik van de tekens.
Oplossen van de laatste vergelijking toont aan dat
$$F_n = mg \cos{\alpha}.$$
Deze normaalkracht is dus minder dan op een horizontale vloer, en neemt af als de helling steiler wordt.
Als er geen wrijving is, dan is de resultante kracht $F_{res} = mg \sin{\alpha}$ positief en versnelt het voorwerp langs de helling omlaag:
$$a = g \sin{\alpha}.$$
Hoe steiler de hellingshoek, des te groter sin α, en des te groter de versnelling.
Als het voorwerp stilstaat op een ruw oppervlak, dan is er statische wrijvingskracht. Wanneer de hellingshoek klein genoeg is, zal deze kracht glijden kunnen tegengaan. Bij hoeken groter dan de kritische hoek gaat het voorwerp glijden. (Hoe groot die kritische hoek is, hangt af van de ruwheid van het oppervlak maar niet van de massa van een voorwerp.)
