Uit paragraaf 20.5 en Newton’s tweede beginsel volgt onmiddellijk dat de centripetaalkracht gelijk is aan
$$F_{cp} = m \ a_{cp} = m \frac{v^2}{r}.$$
hierbij is
- m de massa van het voorwerp, in kilogram (kg);
- v zijn huidige snelheid, in m/s;
- r de straal van de cirkelbaan, in meter (m);
- Fcp de centripetaalkracht, in newtons (N).
Voorbeeld: Een bal met een massa van 0,15 kg rolt door een gootje met een snelheid van 6,0 m/s. Het gootje maakt een (horizontale) bocht, met een krommingsstraal van 0,8 meter. Bepaal de grootte en de richting van de resultante kracht op de bal.
In de bocht is de bal in ECB. De resultante kracht staat dus loodrecht op de beweging, en wijst naar de binnenkant van de bocht. De grootte van de kracht is
$$F_{cp} = m \frac{v^2}{R} = 0,15 \; \text{kg} \cdot \frac{(6,0 \; \text{m/s})^2}{0,8 \; \text{m}} = 0,68 \; \text{N}.$$
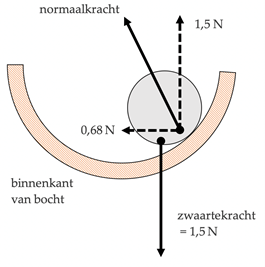
Deze berekening is niet moeilijk; maar het interessant te vragen waar deze centripetale kracht vandaan komt. Op de bal werken slechts twee krachten van belang: de zwaartekracht van de aarde, en de normaalkracht van het gootje. Enerzijds heeft die normaalkracht een verticale component, die de zwaartekracht opheft; anderzijds moet zij een horizontale component hebben, anders zou er geen centripetaalkracht zijn, en zou de bal rechtdoor rollen, door de zijkant van het gootje heen. Dus moet de normaalkracht diagonaal zijn. Omdat de normaalkracht loodrecht op het oppervlak van het oppervlak staat, betekent dit dat de bal zich tijdelijk op de schuine zijkant van het gootje moet bevinden.
