Een harmonische trilling kan worden beschreven door een vergelijking van de vorm:
$$u = A \cdot \sin {(\omega \cdot t + \varphi_0 )}.$$
In deze vergelijking is
- t het tijdstip dat we bestuderen, in seconden (s);
- u de positie of uitwijking op dat moment;
- A de amplitude van de trilling;
- ω de hoeksnelheid, in rad/s (zie hierboven);
- φ0 de fasehoek op tijd t = 0, in radialen (rad).
(De uitdrukking tussen haakjes, $\varphi = \omega \cdot t + \varphi_0$, is de fasehoek op tijdstip t. Deze fasehoek is een lineaire functie van de tijd.)
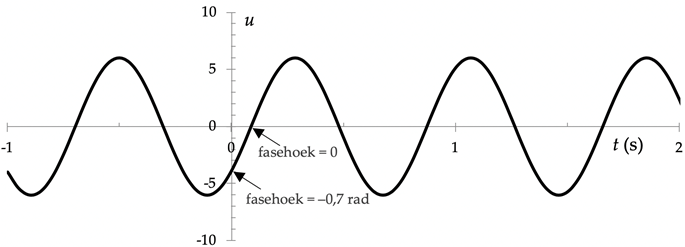
Voorbeeld: Een voorwerp trilt volgens de vergelijking $u = 6 \sin (8 t – 0{,}7)$. Analyseer deze beweging.
Het voorwerp trilt met een amplitude van 6 eenheden.
De hoeksnelheid ω = 8 rad/s. De frequentie en periode zijn derhalve
$$f = \frac{\omega}{2 \pi} = 1{,}27 \;\text{Hz}; \ \ \ T =\frac{2 \pi}{\omega} = 0{,}79 \; \text{s}.$$
De beginfasehoek is –0,7 rad ≈ –40˚; op t = 0 is u dus kleiner dan de evenwichtswaarde, en is aan het toenemen.