Wanneer breking van licht optreedt, zal altijd een deel van het licht gespiegeld worden. Meestal is dit slechts een klein percentage van de totale hoeveelheid licht.
Echter, in een bepaalde situatie treedt totale terugkaatsing op. Het licht kan het grensvlak tussen de twee media dan niet oversteken, maar wordt geheel weerkaatst. Dit gebeurt als uit de wet van Snellius zou volgen dat sin θ’ > 1. De sinus van een hoek kan niet groter dan één zijn; in dit geval is er dus geen oplossing. Er vindt geen breking van licht plaats, maar totale spiegeling.
Wij werken dit verder uit: totale spiegeling treedt alleen op als:
- de brekingsindex van het nieuwe medium kleiner zou zijn ($n’ < n$);
- de invalshoek groter is dan de grenshoek θg, waarvoor $\sin \theta_g > n’/n.$
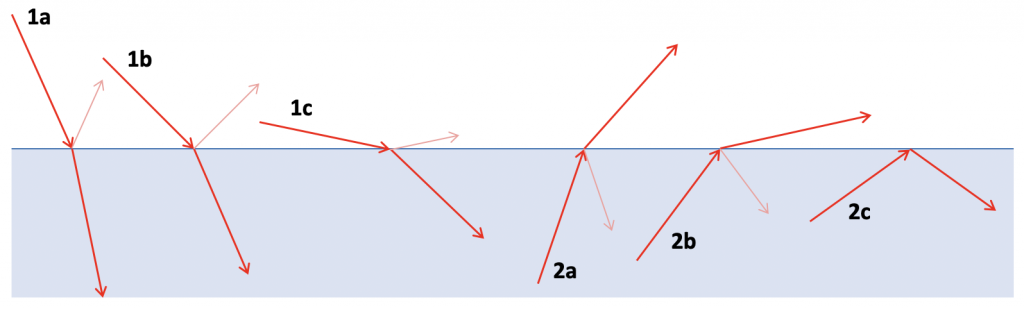
Voorbeeld: Op het grensvlak van lucht en water (n = 1,33) kan totale spiegeling alleen optreden als het licht vanuit het water komt. De grenshoek is in dit geval gelijk aan
$$\text{arc sin} \frac 1 {1{,}33} = 49^\circ.$$
Totale spiegeling treedt dus op voor invalshoeken groter dan 49˚.
