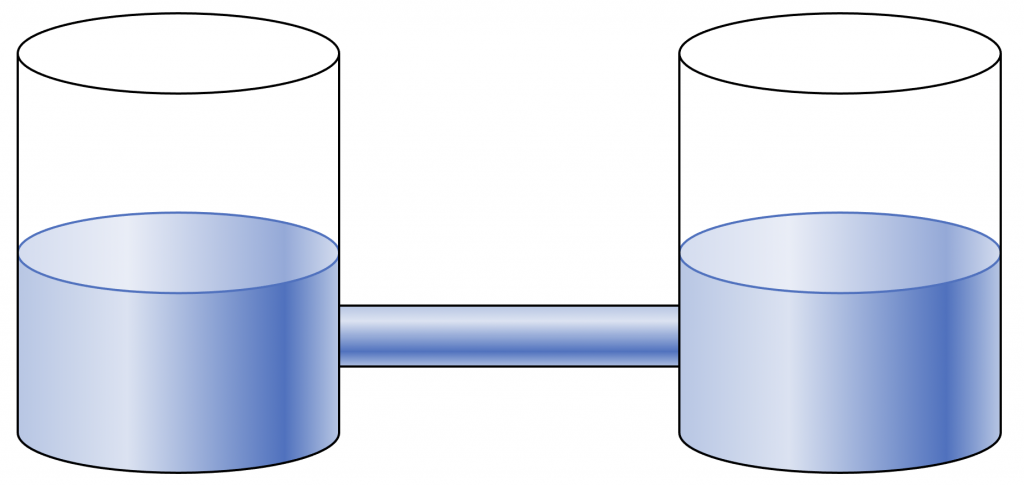
Stel dat twee vaten van onderen verbonden zijn door een pijp, en dat ze deels gevuld worden met een vloeistof. De vloeistof is vrij om door de pijp van het ene vat naar het andere te stromen. Op een gegeven moment zal een evenwicht ontstaan.
In een evenwicht met communicerende vaten is er gelijke druk aan beide zijden van de verbindingspijp.
Dit principe kan men gebruiken om uitspraken te doen over de hoogte of dichtheid van de vloeistof.
(1) Als er maar één soort vloeistof gebruikt wordt, zal de vloeistof in evenwicht overal op dezelfde hoogte staan. Dit is onafhankelijk van de grootte of vorm van de vaten. (Wij gaan er vanuit de vaten zo breed zijn dat capillaire werking geen rol van betekenis speelt.)
Er geldt immers:
$p_L = \rho \cdot g \cdot d_L$ vanaf de linkerkant, en
$ p_R = \rho \cdot g \cdot d_R$ vanaf de rechterkant
en deze drukken moeten gelijk zijn: pL = pR. Hieruit volgt onmiddellijk dat dL = dR.
(2) Stel nu dat bovenop de vloeistof (A) in het rechtervat een andere vloeistof (B) drijft, van lagere dichtheid—bijvoorbeeld olie op water. Nu zal de vloeistofspiegel op verschillende hoogten liggen. In dit geval zal de vloeistof rechts hoger staan dan links:
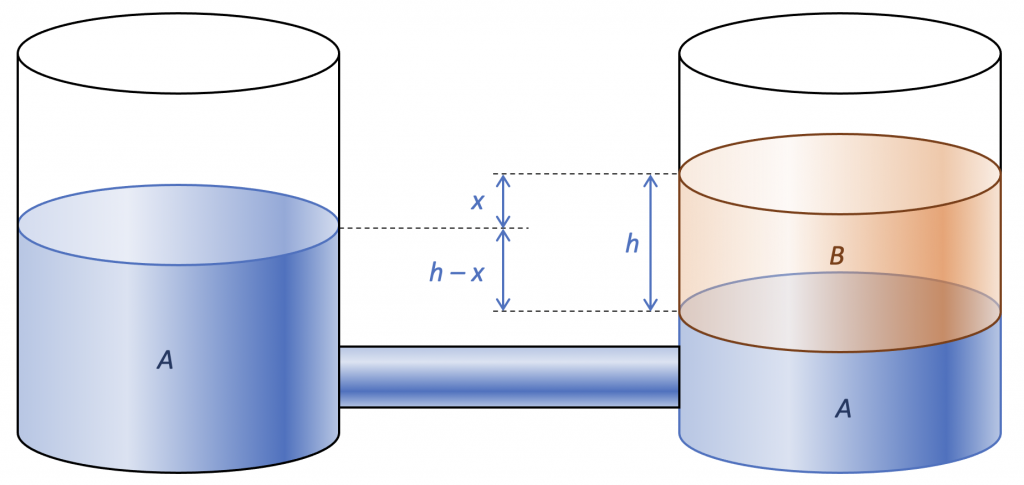
Om dit te analyseren noemen wij de hoogte van vloeistof B “h”, en het hoogteverschil tussen de vloeistofspiegels “x”.
Beschouw punten in beide vaten ter hoogte van het grensvlak tussen A en B. In evenwicht moeten de hydrostatische drukken op die hoogte gelijk in beide vaten. In het rechtervat bevindt zich boven deze hoogte een kolom met vloeistof B ter hoogte h. In het linkervat bevindt zich boven deze hoogte een kolom met vloeistof A ter hoogte h – x. Er geldt dus:
$p_L = \rho_A \cdot g \cdot (h – x)$ aan de linkerkant, en
$p_R = \rho_B \cdot g \cdot h$ aan de rechterkant
Gelijkstelling van deze drukken levert:
$$x=h \cdot \frac{\rho_A – \rho_B}{\rho_A}.$$
Dit is dus hoeveel de vloeistofspiegel in het rechtervat dat hoger staat dan in het linkervat.
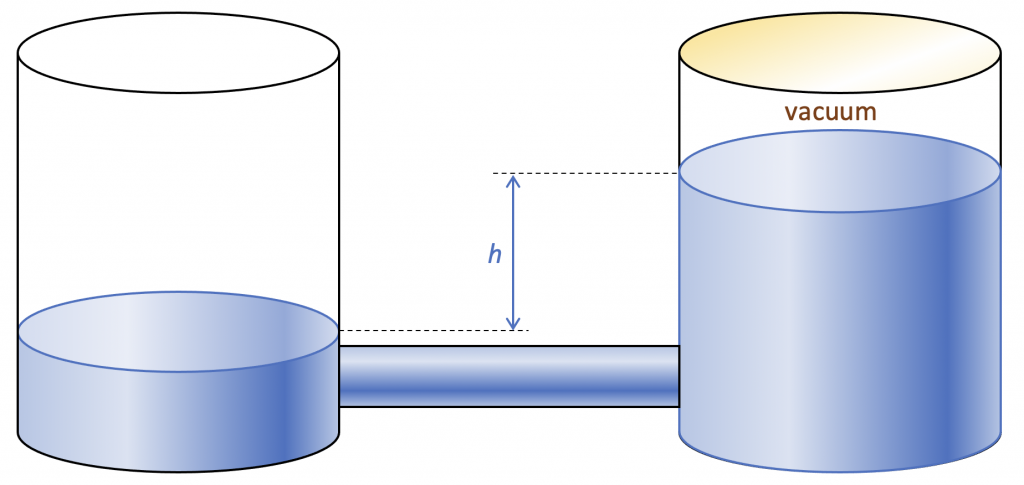
(3) Stel nu dat het rechtervat van boven is afgesloten, en dat de lucht boven de vloeistof daar verwijderd is, zodat een vacuüm ontstaat. Nu zal de vloeistof in het rechtervat (veel) hoger staan dan in het linkervat. De reden hiervoor is dat de luchtdruk de vloeistof aan de linkerkant omlaag drukt, en er aan de rechterkant geen luchtdruk is om tegenwicht te bieden. Dit tegenwicht moet nu komen van de extra vloeistof aan de rechterkant. Omdat deze opstelling gebruikt kan worden om de luchtdruk te meten, staat zij bekend als barometer. Voor de analyse beschouwt men de vloeistoffen ter hoogte van de vloeistofspiegel in het linkervat. De totale drukken moeten daar gelijk zijn. We hebben
$p_L – p_{\text{atmosfeer}}\ $ aan de linkerkant, en
$p_R = \rho \cdot g \cdot h$ aan de rechterkant.
Er volgt onmiddellijk dat
$$p_{\text{atmosfeer}} = \rho \cdot g \cdot h.$$
Voorbeeld: Een traditionele barometer is doorgaans is doorgaans gevuld met kwik, met een dichtheid van 13 600 kg/m3. Het hoogteverschil van de kwik zal gelijk zijn aan
$$h = \frac{p_{\text{atmosfeer}}}{\rho \cdot g} = \frac{101 \; 300 \; \text{Pa}}{13 \; 600 \; \text{kg/m}^3 \cdot 9{,}8 \; \text{N/kg}} = 0{,}76 \; \text{m}.$$
Zo’n barometer zal dus bijna een meter hoog moeten zijn.
Zou men water gebruiken in een barometer, dan krijgt men (nogal onpraktisch!):
$$h = \frac{p_{\text{atmosfeer}}}{\rho \cdot g} = \frac{101 \; 300 \; \text{Pa}}{1000 \; \text{kg/m}^3 \cdot 9{,}8 \; \text{N/kg}} = 10{,}3 \; \text{m}.$$
