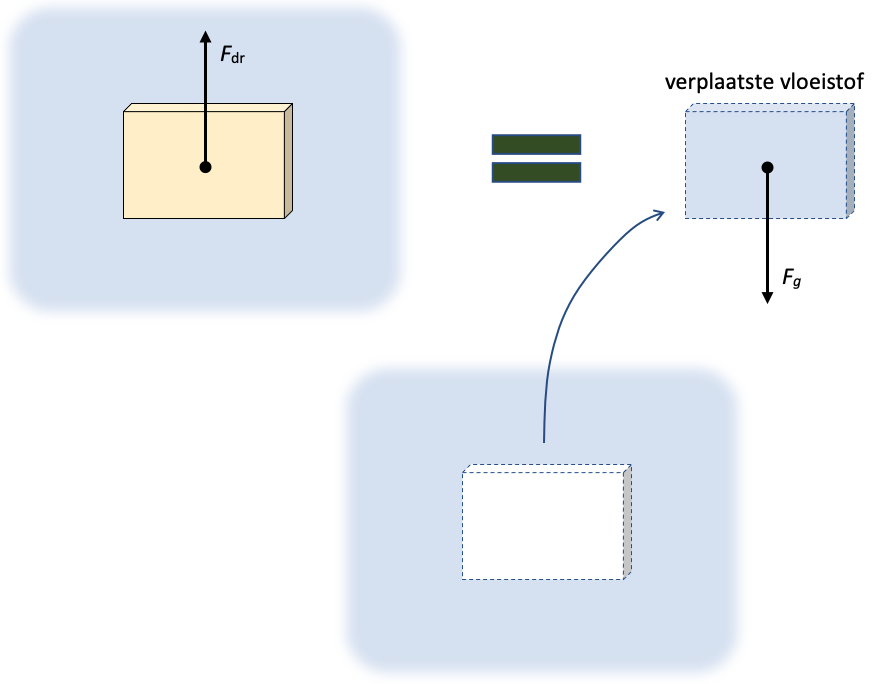
Hoe groot is de drijfkracht op een ondergedompeld voorwerp? Het beginsel van Archimedes stelt dat de drijfkracht gelijk is aan het gewicht van (= de zwaartekracht op) de verplaatste vloeistof.
Wanneer een voorwerp in een vloeistof geplaatst wordt, neemt het de ruimte in die anders door de vloeistof gevuld zou worden. Deze hoeveelheid weggedrukte vloeistof heet verplaatste vloeistof.
Voorbeeld: Een rechthoekig blok met zijden van 40 x 30 x 20 cm wordt ondergedompeld in water. Hoeveel drijfkracht ondervindt het?
Wij berekenen achtereenvolgens het volume, de massa, en de zwaartekracht van het verplaatste water:
$$V = 0{,}40 \cdot 0{,}30 \cdot 0{,}20 = 0{,}024 \; \text{m}^3;$$
$$m = \rho \cdot V = 1000 \; \text{kg/m}^3 \cdot 0{,}024 \; \text{m}^3 = 24 \; \text{kg};$$
$$F_g = m \cdot g = 24 \; \text{kg} \cdot 9{,}8\; \text{N/kg} = 235 \; \mathrm{N}.$$
Volgens het beginsel van Archimedes is de drijfkracht dus 235 N.
Merk op dat de drijfkracht niet afhangt van
- het materiaal waarvan het voorwerp gemaakt is,
- de diepte waarop het gehouden wordt, of
- de oriëntatie in het water.
