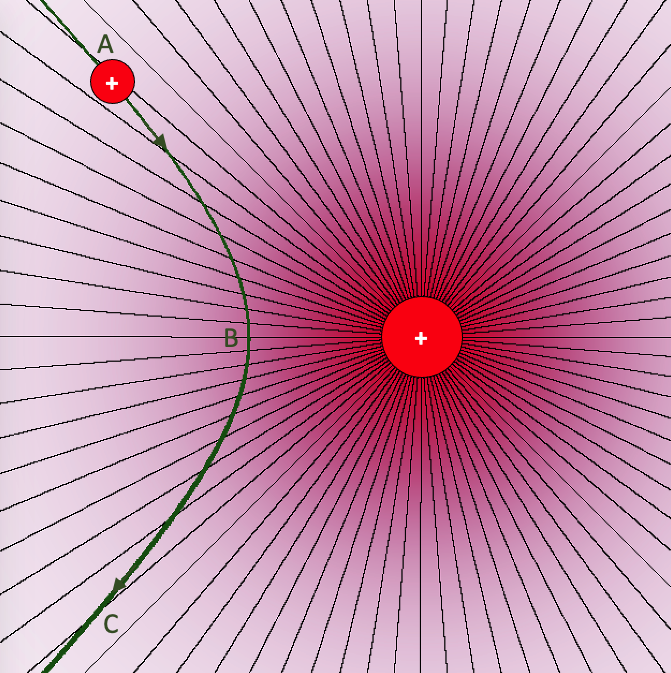
Het diagram laat het veld zien van een positieve bronlading. Een bewegend klein, positief geladen deeltje betreedt dit veld. Door de elektrische afstoting wordt het deeltje afgebogen en beweegt het langs een gekromde (hyperbolische) baan.
Verdere studie laat zien dat het deeltje op traject AB afremt, terwijl het op BC weer sneller gaat bewegen. Uiteindelijk is de snelheid waarmee het vertrekt, gelijk aan de snelheid waarmee het binnenkwam.
Definieer nu twee begrippen:
- De kinetische energie (KE): hoe sneller het deeltje beweegt, des te hoger is zijn KE.
- De (elektrische) potentiële energie (PE): hoe dichter het deeltje bij de bronlading komt, des te hoger is zijn PE.
Het is mogelijk dit zodanig te doen dat de wet van behoud van energie geldt: De totale energie KE + PE van het deeltje verandert niet tijdens deze beweging. In punt A is de KE groter maar de PE kleiner; in punt B is de KE kleiner maar de PE groter; enzovoort.
Voor de kinetische energie van een bewegend voorwerp geldt:
$$\text{KE} = \frac{1}{2} \; m \; v^2$$
Hier is
- KE de kinetische energie, uitgedrukt in joule (J)
- m de massa van het bewegende voorwerp, in kg
- v de snelheid, in m/s.
De elektrische potentiële energie van een lading q in de buurt van een bronlading Q is
$$\text{PE} = k \frac{Q \; q}{d},$$
waarbij (als voorheen) $k = 8{,}99\cdot 10^9\;\mathrm{N\cdot m^2/C^2}$ en d is de afstand tussen de ladingen. (Het verschil met de formule in paragraaf 16.3 is, dat d hier niet gekwadrateerd wordt.) De eenheid van PE is weer de joule (J).
In het geval van aantrekkende ladingen redeneert men net zo, maar nu is de potentiële energie negatief: hoe dichter de testlading bij de aantrekkende bronlading komt, des te kleiner zijn PE en des te groter zijn KE. In dit geval zal het deeltje dus eerst versnellen (AB) en daarna vertragen (BC).
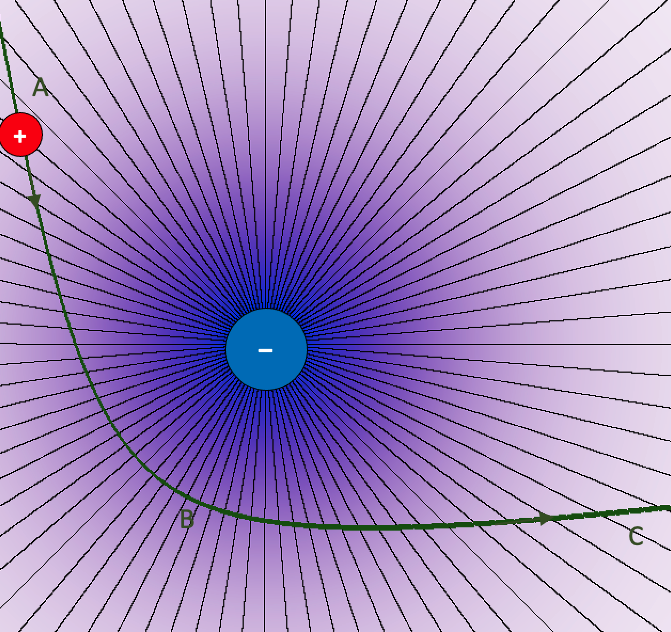
In het algemeen geldt: Als een lading zich beweegt in de richting van de elektrische kracht, neemt de elektrische PE af.
Voorbeeld: Een positief geladen stofdeeltje met een massa van 5,0 g en een lading van 250 nC betreedt het elektrisch veld van een negatief geladen bol (Q = –2,0 μC). Oorspronkelijk had het stofdeeltje een snelheid van 12 m/s. Hoe snel zal het bewegen op een afstand van 3,5 cm van het middelpunt van de bol?
De ladingen trekken elkaar aan. Het stofdeeltje zal dus versnellen: de PE wordt negatief, zodat de KE toeneemt.
Oorspronkelijke KE: $\text{KE}_{\text{voor}} = \frac{1}{2} \cdot (0,0050) \cdot (12)^2 = 0{,}36 \; \text{J}.\ $ (reken g om naar kg)
Oorspronkelijke PE: delen door een grote waarde van d levert $\text{PE}_{\text{voor}} \approx 0 \;\text{J}.$
De totale energie moet nog steeds 0,36 J zijn. Dus geldt voor de nieuwe KE:
$$\text{KE}_{na} = 0{,}36 \; \text{J} \; – \text{PE}_{na} = 0{,}36 \; – (-0{,}13\; \text{J}) = 0{,}49 \; \text{J}.$$
Los nu op: $\frac {1}{2} \cdot 0{,}0050 \cdot v^2 = 0{,}49 \; \text{J}\ $ om de nieuwe snelheid van het deeltje te vinden:
$$v = \sqrt{\frac{2\cdot 0{,}49}{0{,}0050}} = 14 \; \mathrm{m/s}.$$
