Het elektrische veld is homogeen in een gebied als zowel de richting als de sterkte van het E-veld overal gelijk is.
Deze theoretisch meest eenvoudige situatie kan worden benaderd door de vlakke-plaat condensator. Deze bestaat uit twee evenwijdige geleidende platen, waarop gelijke hoeveelheden positieve en negatieve ladingen zijn aangebracht. De veldlijnen lopen loodrecht van de positieve naar de negatieve plaat:
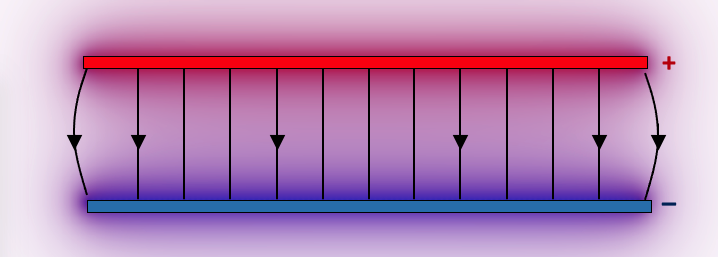
(Aan de randen van de condensator is het veld niet meer homogeen. Dit ziet men aan de gebogen veldlijnen.)
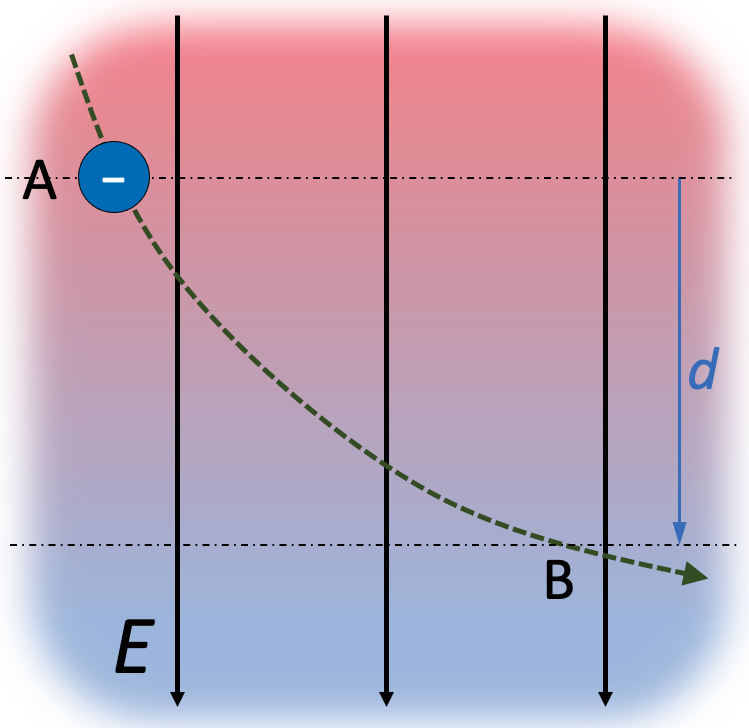
Beschouw nu de volgende situatie: in een homogeen elektrisch veld E bevindt zich een puntlading q die zich van A naar B verplaatst.
De elektrische potentiële energie (PE) zal hierdoor toenemen of afnemen, afhankelijk van de lading van het deeltje en de richting van de beweging.
- Als het deeltje zich beweegt in de richting van de elektrische kracht, neemt de PE af.
(Een (+)-lading met de veldlijnen mee, of een (–)-lading tegen de veldlijnen in.) - Als het deeltje zich beweegt tegen de richting van de elektrische kracht in, neemt de PE toe.
(Een (–)-lading met de veldlijnen mee, of een (+)-lading tegen de veldlijnen in.)
De verandering in de elektrische potentiële energie kan men berekenen als
$$\Delta \text{PE}_E = -q \; E \; d,$$
waarbij
- q de lading van het deeltje is, in C
- E de grootte van het elektrische veld, in N/C
- d de afstand AB gemeten in de richting van de veldlijnen.
Aan de hand van deze potentiële energie kan men vervolgens conclusies trekken over de kinetische energie, en dus de snelheid van het deeltje.
Voorbeeld: Een negatief geladen deeltje (m = 0,020 g; q = –30 μC) wordt een homogeen elektrisch veld (E = 5000 N/C) ingeschoten met een snelheid van 220 m/s, in de richting van de veldlijnen. Hoever zal het deeltje het veld indringen voordat het omkeert?
Omdat de lading negatief is, zal de elektrische kracht tegengesteld zijn aan de veldlijnen. Er is dus een tegenwerkende kracht die het deeltje vertraagt tot het tot stilstand komt. Dat is het punt waarop het deeltje zich zal omkeren.
Het deeltje had oorspronkelijk een kinetische energie van
$$KE_{\text{voor}} = \frac{1}{2} \cdot 0{,}000020 \cdot 220^2 = 0{,}484 \; \mathrm{J}.$$
Wanneer het deeltje omkeert, staat het momentaan stil; dus KEna = 0 J. Het verlies van 0,484 J aan kinetische energie betekent dat het deeltje een winst had van 0,484 J potentiële energie.
Dus lossen wij op:
$$\Delta \text{PE} = -q \; E \; d$$
$$0{,}484 \; \text{J} =\: – (-30 \cdot 10^{-6} \; \text{C}) \cdot (5000 \; \text{N/C}) \cdot d$$
$$d=3{,}23 \; \text{m}.$$
Conclusie: De puntlading zal 3,23 meter diep het veld indringen voor zij tot stilstand komt en omkeert. (Daarna zal zij weer versnellen en het veld verlaten met de beginsnelheid van 220 m/s.)
