Ondanks de immer aanwezige zwaartekracht vallen de meeste voorwerpen toch niet omlaag. Dit komt door een opwaartse kracht die de zwaartekracht tegenwerkt. Meestal is die opwaartse kracht afkomstig van een horizontaal vlak dat het voorwerp ondersteunt. Dit is een voorbeeld van de zgn. normaalkracht.
De normaal kracht wordt uitgeoefend door een hard oppervlak op ieder voorwerp dat door dit oppervlak probeert te dringen. Zij is altijd gericht loodrecht op het oppervlak (dit heet de normaal), en is precies sterk genoeg om het doordringen in het oppervlak te voorkomen.
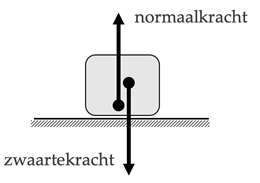
Stel dat een voorwerp op een horizontale plank ligt. Zowel de plank als het voorwerp zijn in rust. Er werken geen andere krachten op het voorwerp: er zijn alleen de zwaartekracht van de aarde (neerwaarts) en de normaalkracht van de plank (opwaarts). Omdat het voorwerp in rust blijft, is het in evenwicht; derhalve hebben de twee krachten gelijke grootte, namelijk $m \cdot g$.
Als de plank het voorwerp omhoogduwt, drukt het voorwerp de plank ook omlaag (Newtons derde beginsel). Deze neerwaartse kracht op een ondersteunend oppervlak heet het gewicht van het voorwerp. Een weegschaal maakt hier gebruik van: eigenlijk meet men de normaalkracht tussen de weegschaal en het gewogen voorwerp. De weegschaal deelt deze door g en presenteert de uitkomst als de massa.
Voorbeeld: Een man met een massa van 95 kg ligt op een luchtbed. Met hoeveel kracht duwt het luchtbed op de man? Met hoeveel kracht duwt de man op het luchtbed?
Volgens Newtons derde beginsel zijn deze twee krachten gelijk. Omdat de man in evenwicht is, moet de opwaartse kracht van het luchtbed wel gelijk zijn aan de zwaartekracht op de man. Dus geldt
$$F = m \; g = 95 \;\text{kg} \cdot 9,8 \;\text{N/kg} = 930 \;\text{N}.$$
