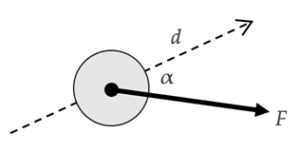
Beschouw een voorwerp dat zich over een afstand d voortbeweegt. Gedurende deze beweging werkt er een kracht F op het voorwerp. Voor het gemak nemen wij aan dat F constant is in grootte en richting.
De arbeid (W) verricht door kracht F op het voorwerp in dit tijdsinterval is
$$W = F_{||} \cdot d \ \ \ \text{of ook} \ \ \ W = F \cdot d \cdot \cos{\alpha}.$$
Hier is F|| = F cos α de krachtcomponent evenwijdig aan de beweging. De SI-eenheid van arbeid en energie is de joule (J). Deze is gedefinieerd als $1 \; \text{J} = 1 \; \mathrm{N\cdot m}.$
Voorbeeld: Een auto van 900 kg rijdt een helling van 30˚ op, over een afstand van 100 meter. De arbeid verricht door de zwaartekracht tijdens dit ritje is
$$W = m \cdot g \cdot d \cdot \cos{\alpha}.$$ $$\; = 900 \; \text{kg} \cdot 9,8 \; \text{N/kg} \cdot 100 \; \text{m} \cdot \cos 120^\circ = -441 \; 000 \; \text{J}.$$
Arbeid kan positief of negatief zijn. Dit is niet omdat arbeid een vectoriële grootheid zou zijn: het teken hangt bijvoorbeeld niet af van het coördinatenstelsel dat wij kiezen.
- De arbeid is positief als de kracht (althans de evenwijdige component) werkt in de bewegingsrichting. Een dergelijke kracht zou dus de neiging hebben de snelheid van het voorwerp te verhogen.
- De arbeid is negatief als de kracht (althans de evenwijdige component) tegengesteld werkt aan de bewegingsrichting. Een dergelijke kracht neigt de snelheid van het voorwerp te verlagen.
- De arbeid is nul als de kracht loodrecht staat op de bewegingsrichting. Een dergelijke kracht heeft geen effect op de snelheid.
Voorbeeld: Een metalen bal van 0,3 kg valt in een diep meer en zinkt naar een diepte van 20 meter. Tijdens dit proces oefent het water 2,0 N opwaartse kracht uit op de bal (drijfkracht en weerstandskracht). Hoeveel arbeid verrichten de verschillende krachten op de bal? Wat is de totale arbeid?
De zwaartekracht verricht positieve arbeid omdat zij werkt in de bewegingsrichting. Het water verricht negatieve arbeid omdat zij de beweging tegenwerkt.
Voor de krachten en de hoeveelheden arbeid vinden wij dus:
$$F_g = m \cdot g \approx 3,0 \; \text{N}; \ \ W_g = F \cdot d = 3,0 \; \text{N} \cdot 20 \; \; \text{m} = 60 \; \text{J};$$
$$F_{\text{water}} = 2,0 \; \text{N}; \ \ W_{\text{water}} = -2,0 \; \text{N} \cdot 20 \; \text{m} = -40 \; \text{J}.$$
De totale arbeid is
$$W_{\text{tot}} = W_g + W_{\text{water}} = 60 + (-40) = 20 \; \text{J}.$$
