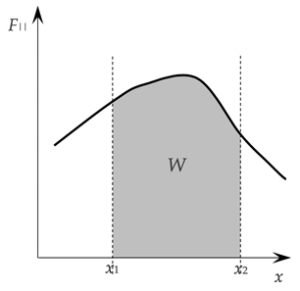
Bij de formule $W = F_{||} \cdot d$ gingen wij ervan uit dat de kracht F constant blijft tijdens de beweging. Als dit niet het geval is, is de berekening van arbeid moeilijker. Een handig hulpmiddel in dat geval is een F(x)-grafiek, waarin de kracht F|| beschreven wordt als functie van de plaats x. Er geldt:
De arbeid verricht door kracht F|| tijdens een verplaatsing van x1 naar x2 is gelijk aan de oppervlakte onder de F(x)-grafiek tussen de verticale lijnen x = x1 en x = x2.
Voorbeeld: Een verhuizer sleept een bank over de vloer over een afstand van vier meter. De grafiek laat zien hoeveel horizontale kracht hij uitoefent op de bank tijdens dit proces. Hoeveel arbeid verricht de verhuizer op de bank?
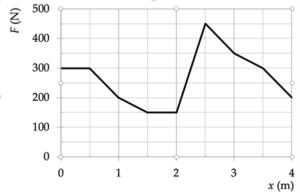
De arbeid is gelijk aan de oppervlakte onder de grafiek. Door tellen vindt men dat deze oppervlakte uit 43 hokjes bestaat. Elk hokje heeft een breedte van 0,5 m en een hoogte van 50 N, zodat
$$1 \; \text{hokje} = 0,5 \; \text{m} \cdot 50 \; \text{N} = 25 \; \text{J}.$$
$$W = 43 \; \text{hokjes} = 43 \cdot 25 \; \text{J} = 1085 \; \text{J}.$$
