In een eerder onderwerp werd de veerkracht behandeld. We zullen nu bespreken hoeveel arbeid verricht wordt bij het uitrekken van een veer.
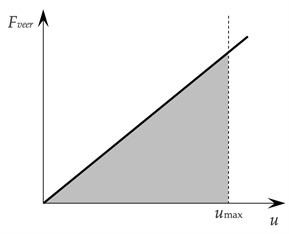
Volgens de wet van Hooke is Fveer = –k u. Hoe verder de veer wordt uitgerekt, des te groter de veerkracht is. Tijdens het uitrekken van een veer is de kracht dus niet constant. Om de verrichte arbeid te bepalen, maken wij gebruik van een F(x)-grafiek. (Deze grafiek is een rechte lijn, waarvan het hellingsgetal gelijk is aan de veerconstante k.)
Stel dat de veer wordt uitgerekt van u = 0 naar een maximumwaarde u = umax. De verrichte arbeid wordt dan gegeven door de driehoekig oppervlakte onder de grafiek. Het is nu niet moeilijk om te zien dat
$$W_\text{veer} = \frac{1}{2} \cdot \text{breedte} \cdot \text{hoogte} = \frac{1}{2} \cdot u_\text{max} \cdot (-k \cdot u_\text{max}).$$ $$W_\text{veer} = \; – \frac{1}{2} k \; u^2_\text{max}.$$
Omdat de veerkracht tegengesteld gericht is aan de uitrekking, verricht de veer negatieve arbeid. Wanneer men de uitgerekte veer loslaat, zal deze spontaan naar ontspannen. Nu verricht de veerkracht positieve arbeid: $W_\text{veer} = \frac{1}{2} k \; u^2_\text{max}.$
Voorbeeld: Hoeveel arbeid moet men verrichten om een veer met k = 1500 N/m uit te rekken over een afstand van 8,0 cm? Hoeveel arbeid verricht de veer als deze terugspringt?
Tijdens het uitrekken verricht negatieve arbeid; wij moeten positieve arbeid verrichten om hem uit te rekken.
$$W = \frac{1}{2} k \; u^2_\text{max} = \frac{1}{2} \cdot 1500 \; \text{N/m} \cdot (0,080 \; \text{m})^2 = 4,8 \; \text{J}.$$
Bij het terugspringen van de veer verricht deze 4,8 J aan arbeid.
Men ziet nu dat een veer als het ware “arbeid kan opslaan”: men moet arbeid op de veer verrichten om deze uit te rekken, maar als de veer zich ontspant geeft het deze arbeid als het ware weer terug. In de volgende paragraaf zullen wij zien dat deze “opgeslagen arbeid” potentiële energie genoemd wordt.
