Stel dat een voorwerp in eenparige cirkelbeweging is, en men van de zijkant tegen deze cirkel aankijkt. Men zal dan slechts één dimensie van de beweging kunnen zien, dat bijvoorbeeld overeenkomt met de x-coördinaat. Deze één-dimensionale projectie van ECB is een harmonische trilling.
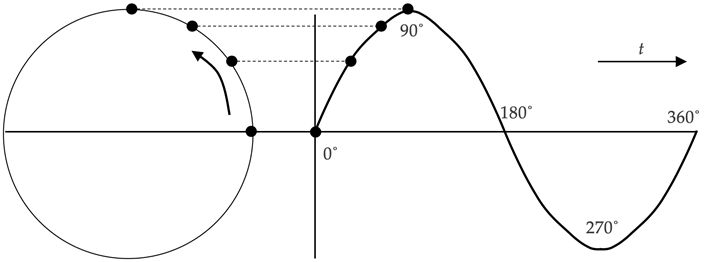
Men kan nu dus de volgende verbanden leggen:
- De periode T van de trilling ~ de omloopstijd T van de ECB.
- De amplitude A van de trilling ~ de staal r van de ECB.
- De maximale snelheid vmax van de trilling ~ de snelheid v van de ECB.
Nu kunnen wij twee extra verbanden leggen:
- De fasehoek φ van de trilling ~ de richtingshoek van de ECB.
- De hoekfrequentie ω van de trilling ~ de hoeksnelheid ω van de ECB.
Toelichting: de fasehoek beschrijft welk deel van de trilling op dit moment wordt uitgevoerd. In één volledige trilling doorloopt de fasehoek 360˚ (ofwel 2π rad).
- φ = 0˚ (0 rad): door de evenwichtspositie in positieve richting.
- φ = 90˚ (½ π rad): grootste positieve waarde bereikt.
- φ = 180˚ (π rad): door de evenwichtspositie in negatieve richting.
- φ = 270˚ (1½ π rad): grootste negatieve waarde bereikt.
- φ = 360˚ (2π rad): volledige trilling uitgevoerd, terug op het 0˚ punt.
De hoekfrequentie ω beschrijft hoe snel de fasehoek toeneemt, en dus hoe snel een trilling doorlopen wordt. De standardeenheid is radialen per seconde (rad/s). Belangrijke formules zijn
$$\omega = \frac{\Delta \varphi}{\Delta t}; \ \ \ \ \ \omega = \frac{2 \pi}{T}; \ \ \ \ \ \omega = 2 \pi f$$
Voorbeeld: Als een veer in trilling is met een periode van 0,20 s, is de hoekfrequentie gelijk aan
$$\omega = \frac{2 \pi}{0,20} = 31 \; \text{rad/s}.$$
