Om de snelheid en versnelling van een harmonische trilling te bepalen, berekent men de eerste en tweede afgeleiden van bovenstaande vergelijking:
$$v= A \omega \cdot \cos{(\omega \cdot t + \varphi_0)};$$
$$a = -A \omega^2 \cdot sin{(\omega \cdot t + \varphi_0)}.$$
De snelheid en versnelling variëren dus ook harmonisch. De amplituden van snelheid en versnelling zijn
$$v_{max} = A \omega; \ \ \ \ \ a_{max} = A \omega^2. $$
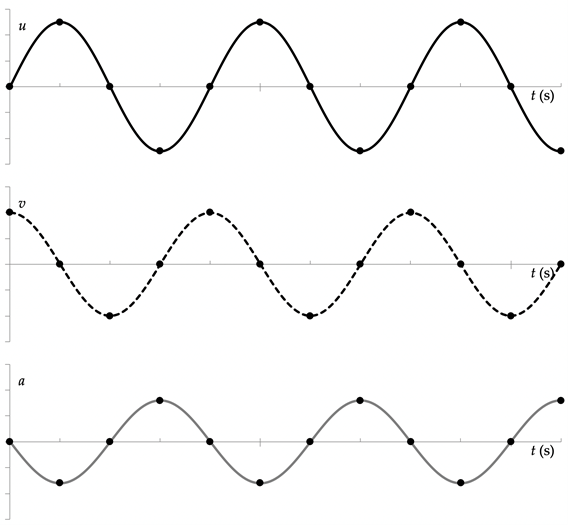
De formule voor de snelheid heeft een cosinus in plaats van een sinus: dit geeft aan dat de snelheid 90˚ in fase “voorloopt”. Zo is de snelheid maximaal of minimaal wanneer het voorwerp zich in de evenwichtstoestand bevindt, en nul wanneer het voorwerp een verste punt bereikt.
Voorbeeld: Een blok hangt aan een veer en trilt met een frequentie van 7 Hz en een amplitude van 1,2 cm. Wat is de maximumsnelheid van het blok?
Wij hebben te maken met harmonische trilling met $A = 1{,}2 \; \text{cm}$ en $\omega = 2 \pi f = 2 \pi \cdot 7 = 44 \; \text{rad/s}$. Dus is
$$v_{max} = A \omega = 1{,}2 \cdot 44 = 53 \; \text{cm}.$$
