Als één punt van een medium in periodieke beweging wordt gebracht, zullen uiteindelijk alle punten een dergelijke beweging uitvoeren. In een periodieke golf voert dus ieder punt dezelfde beweging herhaaldelijk uit. Een bijzonder geval hiervan is de harmonische golf, waar ieder punt een harmonische trilling uitvoert.
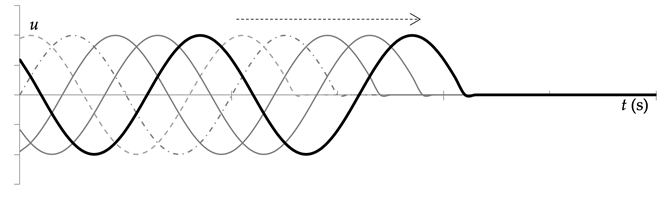
Als men een momentopname maakt van ene periodieke golf, ziet men een patroon dat zich ook herhaalt in de ruimte. De afstand waarover deze herhaling plaatsvindt (bijv. de afstand tussen twee opeenvolgende “pieken”) heet de golflengte (λ).
De golflengte λ beschrijft het ruimtelijk aspect van de periodieke golf, net zoals de periode T het tijdsaspect beschrijft. Het verband tussen deze twee is
$$v = \frac{\lambda}{T},$$
waarbij v de golfsnelheid is. In de praktijk wordt in plaats van de periode vaak de frequentie gegeven; dan gebruikt men
$$v = f \cdot \lambda.$$
Voorbeeld: De pieken van opeenvolgende golven in een diep meer hebben een afstand van 6,0 m. De golven planten zich voort met een snelheid van 3,1 m/s. Wat zijn de periode en frequentie van de golfbeweging?
$$T=\frac{\lambda}{v} = \frac{6{,}0 \; \text{m}}{3{,}1 \; \text{m/s}} = 1{,}93 \; \text{s}.$$
$$f = \frac{v}{\lambda} = \frac{3{,}1 \; \text{m/s}}{6{,}0 \; \text{m}} = 0{,}52 \; \text{Hz}.$$
