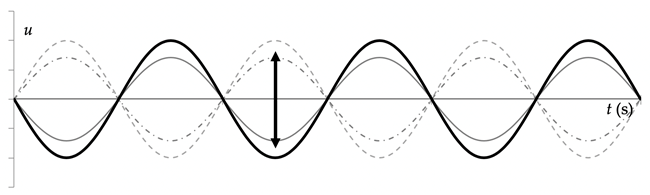
In een staande golf zijn twee soorten bijzondere punten te onderscheiden.
- knopen: punten waar de amplitude van de trilling gelijk is aan nul. Hier is de interferentie steeds volmaakt destructief.
- buiken: punten waar de amplitude van de trilling maximaal is. Hier is de interferentie steeds volmaakt constructief.
De kopen en buiken wisselen elkaar af op een afstand van een kwart golflengte. (De afstand tussen twee opeenvolgende knopen is dus een halve golflengte.)
Voorbeeld: In een 10 meter lang touw bestaat een staand golfpatroon, met een knoop aan elk van de uiteinden, en nog 6 knopen daartussen. Bepaal de golflengte.
Door de situatie te tekenen ziet men dat er zeven knoop-knoop afstanden zijn. Derhalve is λ/2 = L/7; ofwel,
$$\lambda = \frac{2L}{7} = \frac{2 \cdot 10 \; \text{m}}{7} = 2{,}8 \; \text{m}.$$
