Een asymptoot is een lijn waar de grafiek van f steeds dichterbij komt, zonder deze echt te raken. Dit houdt verband met limieten.
- Een verticale asymptoot treedt op bij een “gat” in het domein als de limietwaarde gelijk is aan +∞ of –∞.
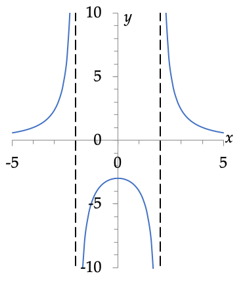
De functie
$$f(x) = \frac{12}{x^2-4}$$
heeft twee “gaten”, namelijk als x = –2 en als x = 2. Uit de grafiek ziet men dat voor deze waarden verticale asymptoten optreden. Dit komt overeen met de volgende limieten:
$$\lim_{x\uparrow-2}f(x) = + \infty, \;\;\;\; \lim_{x\downarrow -2} f(x) = – \infty,$$ $$\lim_{x\uparrow 2} f(x) = – \infty \;\;\;\; \lim_{x \downarrow2} f(x) = + \infty$$
- Een horizontale asymptoot treedt op als de limieten voor $x\rightarrow + \infty$ of $- \infty$ een eindige waarde hebben.
De functie
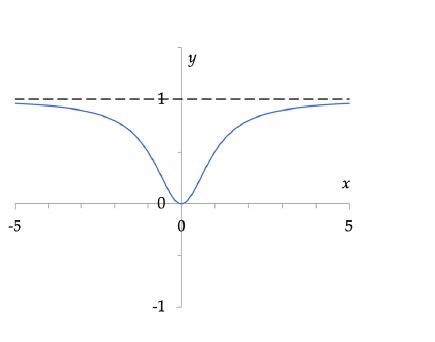
$$f(x) = \frac{x^2}{x^2 + 1}$$
heeft als limiet , $\lim_{x \rightarrow + \infty$ zoals men in de tabel kan zien.
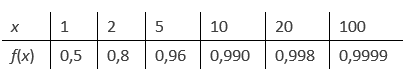
Dus is de lijn y = 1 een horizontale asymptoot.
- Een schuine asymptoot treedt op als een functie in de limiet <$ x \rightarrow +\infty$ of $-\infty$ steeds dichter een lineaire functie benadert.
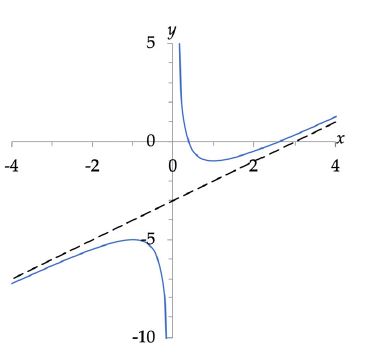
De functie $f(x) = \frac{x^2 – 3x + 1}{x}$$
heeft de lijn y = x – 3 als schuine asymptoot .
Voor verdere details, zie de bespreking van rationele functies in paragraaf 40.4.
