Beschouw een functie van het type $$f(x) = A \cdot \sin K(x-B) + C$$
Hier is
- C de evenwichtswaarde waarom f(x) heen en weer beweegt.
- A de amplitude, die aangeeft hoeveel f(x) maximaal afwijkt van de evenwichtswaarde.
- K de “hoekfrequentie” of het “golfgetal”. Hoe groter K is, des te “sneller” gaat de functie op en neer.
- De periode T is de afstand waarover f(x) zich herhaalt. Er geldt: $$K = \frac{2\pi}{T}.$$
- B de waarde waar het “begin” van het patroon te vinden is.
- Het “begin” van sinusfunctie is schuin omhoog vanuit de evenwichtspositie.
- Het “begin” van cosinusfunctie is bij de maximumwaarde.
Aan de hand van deze eigenschappen kan men bij een beschrijving (bijv. de grafiek) een functievoorschrift opstellen.
Bepaal een functievoorschrift voor onderstaande grafiek.
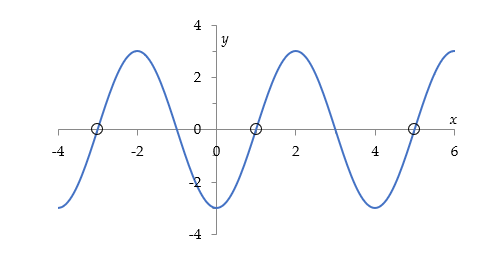
o De grafiek beweegt zich symmetrisch rond de x-as, dus de evenwichtsstand is C = 0.
o De grafiek wijkt maximaal drie eenheden daarvan af, dus de amplitude is A = 3.
o Het patroon begint opnieuw na elke vier eenheden. Dus de periode is $T= 4$ en $K = \frac{\pi}{2}$.
o Als we dit als sinusfunctie schrijven, ligt het beginpunt in de evenwichtsstand met omhooggaande lijn. Dit is bijvoorbeeld het geval bij x = 1. Dus B = 1.
o Al met al,
$f(x) = 3 \sin{\frac{\pi}{2}}(x-1).$
- Andere mogelijkheden zijn bijv.
$f(X) = 3 \sin{\frac{\pi}{2}}(x + 3)$ of $- \cos{\frac{\pi x}{2}}.$
