De zwaartekracht (Fg) op elk voorwerp op aarde bedraagt 9,8 N voor elke kilogram aan massa. Ofwel,
$$F_g=m \cdot g\ \ \ \ \ \ \text{met}\ g = 9{,}8\; \text{N/kg}.$$
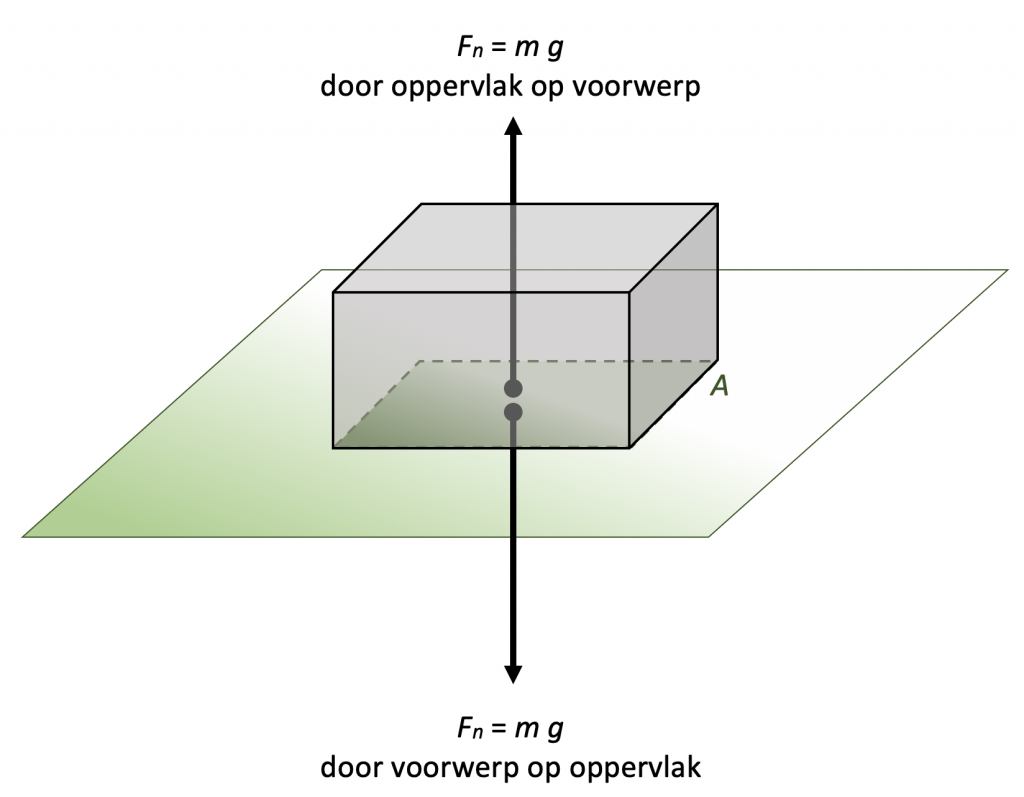
Wanneer een voorwerp op de grond staat of ligt, trekt de zwaartekracht eraan met een neerwaartse kracht $m\:g$. De grond houdt het voorwerp in evenwicht door terug te duwen met een even grote kracht. Deze normaalkracht tussen grond en voorwerp betekent dus dat zij druk op elkaar uitoefenen.
Voorbeeld: Een olifant van 1000 kg heeft vier poten, elk met een oppervlakte van 1 m2. Een dame van 55 kg draagt twee schoenen met hoge hakken, waarvan elk de grond raakt op een oppervlakte van 2 cm2. Vergelijk de druk die ontstaat tussen de grond en elk van hen.
De kracht die de grond op elk van hen uitoefent is gelijk aan de zwaartekracht, $m\:g$. Zo vinden wij voor de olifant 9800 N en voor de dame 540 N aan kracht. De oppervlakten zijn respectievelijk 4 m2 en 4 cm2 = 0,0004 m2.
$$P_{\text{olifant}} = \frac{9800 \; \text{N}}{4 \; \text{m}^2} = 2\;450 \; \text{Pa};$$
$$P_{\text{dame}} = \frac{540 \; \text{N}}{0{,}0004 \; \text{m}^2}=1\;350\;000 \; \text{Pa}.$$
De druk onder de hakken is dus veel groter dan die onder de poten van de olifant!
(Opmerking: In gevallen als deze negeren wij de luchtdruk, omdat die aan alle kanten gelijkelijk op een voorwerp drukt. Dezer krachten heffen elkaar voornamelijk op.)
