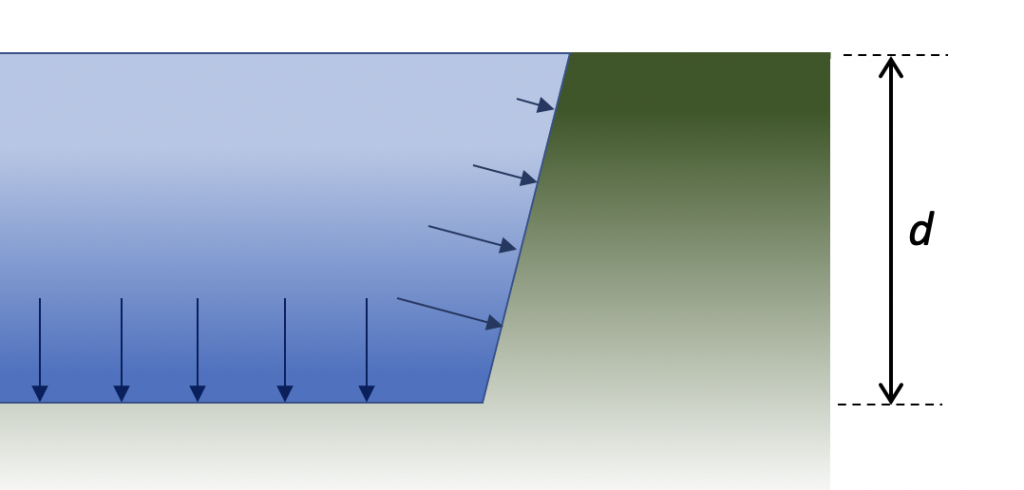
Als men dieper in water (of een andere vloeistof) duikt, neemt de druk toe, vanwege het gewicht van het bovenliggende water. Maakt men gebruik van bovenstaande definities, dan vindt men voor de vloeistofdruk (ofwel hydrostatische druk) op diepte d:
$$p_{hs}=\rho \cdot g \cdot d.$$
Hierbij is
- $\rho$ de dichtheid van de vloeistof, in kg/m3; deze wordt constant verondersteld.
Voor water heeft men bijvoorbeeld \$rho = 1000\;\text{kg/m}3$. - g = 9,8 N/kg (op aarde);
- d de diepte onder het vloeistofoppervlak, in meter (m);
- phs de hydrostatische druk op die diepte, in pascal (Pa).
Voor de totale druk in een vloeistof zou men hier nog de omringende luchtdruk moeten bijtellen:
$$\text{totale druk} = \text{hydrostatische druk} + \text{luchtdruk}.$$
Voorbeeld: Wat is de druk op de bodem van een zwembad van 3,0 meter diep?
hydrostatische druk = $\rho \cdot g \cdot d = 1000 \; \text{kg/m}^3 \cdot 9{,}8 \; \text{N/kg} \cdot 3,0 \; \text{m} = 29 \, 400 \; \text{Pa};$
totale druk = 29 400 Pa + 101 300 Pa = 130 700 Pa.
Op deze diepte is de druk dus ongeveer 30% hoger dan de gewone luchtdruk.
